Data parallelism

Data parallelism is parallelization across multiple processors in parallel computing environments. It focuses on distributing the data across different nodes, which operate on the data in parallel. It can be applied on regular data structures like arrays and matrices by working on each element in parallel. It contrasts to task parallelism as another form of parallelism.

A data parallel job on an array of n elements can be divided equally among all the processors. Let us assume we want to sum all the elements of the given array and the time for a single addition operation is Ta time units. In the case of sequential execution, the time taken by the process will be n×Ta time units as it sums up all the elements of an array. On the other hand, if we execute this job as a data parallel job on 4 processors the time taken would reduce to (n/4)×Ta + merging overhead time units. Parallel execution results in a speedup of 4 over sequential execution. One important thing to note is that the locality of data references plays an important part in evaluating the performance of a data parallel programming model. Locality of data depends on the memory accesses performed by the program as well as the size of the cache.

Exploitation of the concept of data parallelism started in 1960s with the development of the Solomon machine.^[1] The Solomon machine, also called a vector processor, was developed to expedite the performance of mathematical operations by working on a large data array (operating on multiple data in consecutive time steps). Concurrency of data operations was also exploited by operating on multiple data at the same time using a single instruction. These processors were called 'array processors'.^[2] In the 1980s, the term was introduced ^[3] to describe this programming style, which was widely used to program Connection Machines in data parallel languages like C*. Today, data parallelism is best exemplified in graphics processing units (GPUs), which use both the techniques of operating on multiple data in space and time using a single instruction.

Most data parallel hardware supports only a fixed number of parallel levels, often only one. This means that within a parallel operation it is not possible to launch more parallel operations recursively, and means that programmers cannot make use of nested hardware parallelism. The programming language NESL was an early effort at implementing a nested data-parallel programming model on flat parallel machines, and in particular introduced the flattening transformation that transforms nested data parallelism to flat data parallelism. This work was continued by other languages such as Data Parallel Haskell and Futhark, although arbitrary nested data parallelism is not widely available in current data-parallel programming languages.

In a multiprocessor system executing a single set of instructions (SIMD), data parallelism is achieved when each processor performs the same task on different distributed data. In some situations, a single execution thread controls operations on all the data. In others, different threads control the operation, but they execute the same code.

For instance, consider matrix multiplication and addition in a sequential manner as discussed in the example.

Below is the sequential pseudo-code for multiplication and addition of two matrices where the result is stored in the matrix C. The pseudo-code for multiplication calculates the dot product of two matrices A, B and stores the result into the output matrix C.

If the following programs were executed sequentially, the time taken to calculate the result would be of the ${\displaystyle O(n^{3})}$(assuming row lengths and column lengths of both matrices are n) and ${\displaystyle O(n)}$for multiplication and addition respectively.

// Matrix multiplication
for (i = 0; i < row_length_A; i++)
{		
    for (k = 0; k < column_length_B; k++)
    {
        sum = 0;
        for (j = 0; j < column_length_A; j++)
        {
            sum += A[i][j] * B[j][k];
        }
        C[i][k] = sum;
    }
}

// Array addition
for (i = 0; i < n; i++) {
    c[i] = a[i] + b[i];
}

We can exploit data parallelism in the preceding code to execute it faster as the arithmetic is loop independent. Parallelization of the matrix multiplication code is achieved by using OpenMP. An OpenMP directive, "omp parallel for" instructs the compiler to execute the code in the for loop in parallel. For multiplication, we can divide matrix A and B into blocks along rows and columns respectively. This allows us to calculate every element in matrix C individually thereby making the task parallel. For example: A[m x n] dot B [n x k] can be finished in ${\displaystyle O(n)}$ instead of ${\displaystyle O(m*n*k)}$ when executed in parallel using m*k processors.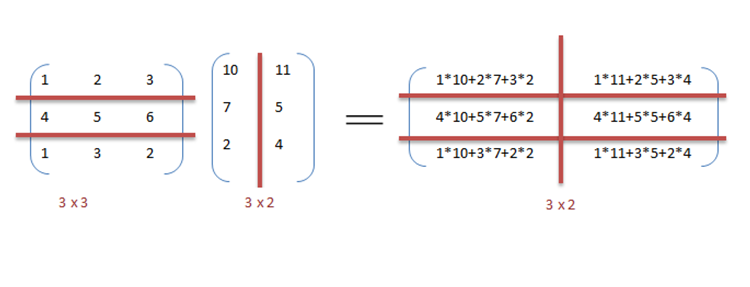

// Matrix multiplication in parallel
#pragma omp parallel for schedule(dynamic,1) collapse(2)
for (i = 0; i < row_length_A; i++){
    for (k = 0; k < column_length_B; k++){
        sum = 0;
        for (j = 0; j < column_length_A; j++){
            sum += A[i][j] * B[j][k];
        }
        C[i][k] = sum;
    }
}

It can be observed from the example that a lot of processors will be required as the matrix sizes keep on increasing. Keeping the execution time low is the priority but as the matrix size increases, we are faced with other constraints like complexity of such a system and its associated costs. Therefore, constraining the number of processors in the system, we can still apply the same principle and divide the data into bigger chunks to calculate the product of two matrices.^[4]

For addition of arrays in a data parallel implementation, let's assume a more modest system with two central processing units (CPU) A and B, CPU A could add all elements from the top half of the arrays, while CPU B could add all elements from the bottom half of the arrays. Since the two processors work in parallel, the job of performing array addition would take one half the time of performing the same operation in serial using one CPU alone.

The program expressed in pseudocode below—which applies some arbitrary operation, foo, on every element in the array d—illustrates data parallelism:^{[nb 1]}

if CPU = "a" then
    lower_limit := 1
    upper_limit := round(d.length / 2)
else if CPU = "b" then
    lower_limit := round(d.length / 2) + 1
    upper_limit := d.length

for i from lower_limit to upper_limit by 1 do
    foo(d[i])

In an SPMD system executed on 2 processor system, both CPUs will execute the code.

Data parallelism emphasizes the distributed (parallel) nature of the data, as opposed to the processing (task parallelism). Most real programs fall somewhere on a continuum between task parallelism and data parallelism.

The process of parallelizing a sequential program can be broken down into four discrete steps.^[5]

^[6]

Data and task parallelism, can be simultaneously implemented by combining them together for the same application. This is called Mixed data and task parallelism. Mixed parallelism requires sophisticated scheduling algorithms and software support. It is the best kind of parallelism when communication is slow and number of processors is large.^[7]

Mixed data and task parallelism has many applications. It is particularly used in the following applications:

1. Mixed data and task parallelism finds applications in the global climate modeling. Large data parallel computations are performed by creating grids of data representing Earth's atmosphere and oceans and task parallelism is employed for simulating the function and model of the physical processes.
2. In timing based circuit simulation. The data is divided among different sub-circuits and parallelism is achieved with orchestration from the tasks.

A variety of data parallel programming environments are available today, most widely used of which are:

1. Message Passing Interface: It is a cross-platform message passing programming interface for parallel computers. It defines the semantics of library functions to allow users to write portable message passing programs in C, C++ and Fortran.
2. Open Multi Processing^[8] (Open MP): It's an Application Programming Interface (API) which supports shared memory programming models on multiple platforms of multiprocessor systems. Since version 4.5, OpenMP is also able to target devices other than typical CPUs. It can program FPGAs, DSPs, GPUs and more. It is not confined to GPUs like OpenACC.
3. CUDA and OpenACC: CUDA and OpenACC (respectively) are parallel computing API platforms designed to allow a software engineer to utilize GPU's computational units for general purpose processing.
4. Threading Building Blocks and RaftLib: Both open source programming environments that enable mixed data/task parallelism in C/C++ environments across heterogeneous resources.

Data parallelism finds its applications in a variety of fields ranging from physics, chemistry, biology, material sciences to signal processing. Sciences imply data parallelism for simulating models like molecular dynamics,^[9] sequence analysis of genome data ^[10] and other physical phenomenon. Driving forces in signal processing for data parallelism are video encoding, image and graphics processing, wireless communications ^[11] to name a few.

• Active message
• Instruction level parallelism
• Parallel programming model
• Prefix sum
• Scalable parallelism
• Segmented scan
• Thread level parallelism

• Hillis, W. Daniel and Steele, Guy L., Data Parallel Algorithms Communications of the ACM December 1986
• Blelloch, Guy E, Vector Models for Data-Parallel Computing MIT Press 1990. ISBN 0-262-02313-X