Rectangular mask short-time Fourier transform
In mathematics and Fourier analysis , a rectangular mask short-time Fourier transform (rec-STFT) has the simple form of short-time Fourier transform . Other types of the STFT may require more computation time than the rec-STFT.
The rectangular mask function can be defined for some bound (B) over time (t ) as
w
(
t
)
=
{
1
;
|
t
|
≤
B
0
;
|
t
|
>
B
{\displaystyle w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}}
B = 50, x -axis (sec)We can change B for different tradeoffs between desired time resolution and frequency resolution.
Rec-STFT
X
(
t
,
f
)
=
∫
t
−
B
t
+
B
x
(
τ
)
e
−
j
2
π
f
τ
d
τ
{\displaystyle X(t,f)=\int _{t-B}^{t+B}x(\tau )e^{-j2\pi f\tau }\,d\tau }
Inverse form
x
(
t
)
=
∫
−
∞
∞
X
(
t
1
,
f
)
e
j
2
π
f
t
d
f
where
t
−
B
<
t
1
<
t
+
B
{\displaystyle x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ where }}t-B<t_{1}<t+B}
Property
Rec-STFT has similar properties with Fourier transform
(a)
∫
−
∞
∞
X
(
t
,
f
)
d
f
=
∫
t
−
B
t
+
B
x
(
τ
)
∫
−
∞
∞
e
−
j
2
π
f
τ
d
f
d
τ
=
∫
t
−
B
t
+
B
x
(
τ
)
δ
(
τ
)
d
τ
=
{
x
(
0
)
;
|
t
|
<
B
0
;
otherwise
{\displaystyle \int _{-\infty }^{\infty }X(t,f)\,df=\int _{t-B}^{t+B}x(\tau )\int _{-\infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{t-B}^{t+B}x(\tau )\delta (\tau )\,d\tau ={\begin{cases}\ x(0);&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}
(b)
∫
−
∞
∞
X
(
t
,
f
)
e
−
j
2
π
f
v
d
f
=
{
x
(
v
)
;
v
−
B
<
t
<
v
+
B
0
;
otherwise
{\displaystyle \int _{-\infty }^{\infty }X(t,f)e^{-j2\pi fv}\,df={\begin{cases}\ x(v);&v-B<t<v+B\\\ 0;&{\text{otherwise}}\end{cases}}}
Shifting property (shift along x-axis)
∫
t
−
B
t
+
B
x
(
τ
+
τ
0
)
e
−
j
2
π
f
τ
d
τ
=
X
(
t
+
τ
0
,
f
)
e
j
2
π
f
τ
0
{\displaystyle \int _{t-B}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}}
Modulation property (shift along y -axis)
∫
t
−
B
t
+
B
[
x
(
τ
)
e
j
2
π
f
0
τ
]
d
τ
=
X
(
t
,
f
−
f
0
)
{\displaystyle \int _{t-B}^{t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})}
When
x
(
t
)
=
δ
(
t
)
,
X
(
t
,
f
)
=
{
1
;
|
t
|
<
B
0
;
otherwise
{\displaystyle x(t)=\delta (t),X(t,f)={\begin{cases}\ 1;&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}
When
x
(
t
)
=
1
,
X
(
t
,
f
)
=
2
B
sinc
(
2
B
f
)
e
j
2
π
f
t
{\displaystyle x(t)=1,X(t,f)=2B\operatorname {sinc} (2Bf)e^{j2\pi ft}}
If
h
(
t
)
=
α
x
(
t
)
+
β
y
(
t
)
{\displaystyle h(t)=\alpha x(t)+\beta y(t)\,}
H
(
t
,
f
)
,
X
(
t
,
f
)
,
{\displaystyle H(t,f),X(t,f),}
Y
(
t
,
f
)
{\displaystyle Y(t,f)\,}
H
(
t
,
f
)
=
α
X
(
t
,
f
)
+
β
Y
(
t
,
f
)
.
{\displaystyle H(t,f)=\alpha X(t,f)+\beta Y(t,f).}
Power integration property
∫
−
∞
∞
|
X
(
t
,
f
)
|
2
d
f
=
∫
t
−
B
t
+
B
|
x
(
τ
)
|
2
d
τ
{\displaystyle \int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{t-B}^{t+B}|x(\tau )|^{2}\,d\tau }
∫
−
∞
∞
∫
−
∞
∞
|
X
(
t
,
f
)
|
2
d
f
d
t
=
2
B
∫
−
∞
∞
|
x
(
τ
)
|
2
d
τ
{\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df\,dt=2B\int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau }
∫
−
∞
∞
X
(
t
,
f
)
Y
∗
(
t
,
f
)
d
f
=
∫
t
−
B
t
+
B
x
(
τ
)
y
∗
(
τ
)
d
τ
{\displaystyle \int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df=\int _{t-B}^{t+B}x(\tau )y^{*}(\tau )\,d\tau }
∫
−
∞
∞
∫
−
∞
∞
X
(
t
,
f
)
Y
∗
(
t
,
f
)
d
f
d
t
=
2
B
∫
−
∞
∞
x
(
τ
)
y
∗
(
τ
)
d
τ
{\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df\,dt=2B\int _{-\infty }^{\infty }x(\tau )y^{*}(\tau )\,d\tau }
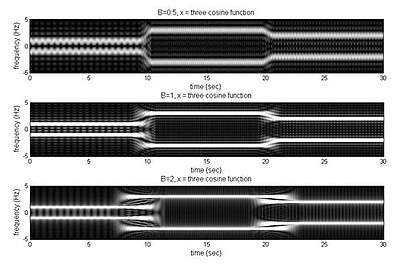
Example of tradeoff with different B
Spectrograms produced from applying a rec-STFT on a function consisting of 3 consecutive cosine waves. (top spectrogram uses smaller B of 0.5, middle uses B of 1, and bottom uses larger B of 2.)From the image, when B is smaller, the time resolution is better. Otherwise, when B is larger, the frequency resolution is better.
Advantage and disadvantage
Compared with the Fourier transform:
Advantage: The instantaneous frequency can be observed.Disadvantage: Higher complexity of computation.Compared with other types of time-frequency analysis :
Advantage: Least computation time for digital implementation.Disadvantage: Quality is worse than other types of time-frequency analysis. The jump discontinuity of the edges of the rectangular mask results in Gibbs ringing artifacts in the frequency domain, which can be alleviated with smoother windows .
See also
References
Jian-Jiun Ding (2014) Time-frequency analysis and wavelet transform







![{\displaystyle \int _{t-B}^{t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499bbda6d65061b339311284633b2fad5774cc94)









